1. 추론통계
(1) 가설검정
- 대표적인 예로 기억하는게 제일 쉽더라고요! ADSP공부할 때 1등으로 등장한 무죄 추정의 원칙으로 생각하는게 가장 쉽더라고요!
| 귀무가설( H₀) | 민수는 범인이 아니야 |
| 대립가설( H₁) | 민수는 범인이야 |
| 유의수준( α) | 민수가 실제로 무죄인데도, 잘못 유죄로 판단할 확률 |
(2) 신뢰구간
- 모집단의 평균을 포함할 가능성이 높은 값의 범위를 제공하는 개념
즉, 값이 이 범위 안에 있을거라고 믿을 수 있는 범위구간

이렇게 헷갈리는 개념이나 예시가 궁금할 때 chatgpt에게 신뢰구간을 물어보고 이와 관련된 초등학생도 이해하기 쉬운 수준으로 알려줘라고 하면 쉽게 알려줘요?!하하 저는 이렇게 이해를 하곤 했답니다:)
(3) 회귀분석
- 단순 선형 회귀: 하나의 독립변수가 종속변수에 미치는 영향을 분석하는 모델
x는 독립변수, Y는 종속변수, a는 기울기, b는 y절편
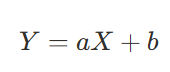
import numpy as np
from sklearn.linear_model import LinearRegression
# 데이터 준비
visit = np.array([5, 10, 15, 20, 25]).reshape(-1, 1)
time = np.array([30, 60, 90, 120, 150]).reshape(-1, 1)
cart = np.array([1, 3, 5, 7, 9]).reshape(-1, 1)
purchase = np.array([50, 80, 120, 160, 200])
# 단순 회귀 (방문 횟수)
model_visit = LinearRegression().fit(visit, purchase)
coef_visit = model_visit.coef_[0]
# 단순 회귀 (체류 시간)
model_time = LinearRegression().fit(time, purchase)
coef_time = model_time.coef_[0]
print(f"방문 횟수 계수: {coef_visit:.2f}")
print(f"체류 시간 계수: {coef_time:.2f}")
- 다중 선형 회귀: 여러 개의 독립변수가 종속변수에 영향을 미치는 모델
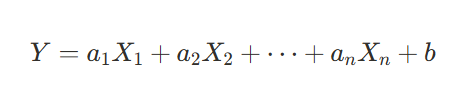
(4) T-검정
: 두 집단 간의 평균 차이가 통계적으로 유의미한지 여부를 검정
- 독립표본 T- 검정
# A/B 테스트
group_A = [8.1, 9.0, 7.5, 8.7, 9.2, 8.3, 8.9] # 기존 디자인
group_B = [10.5, 11.2, 10.8, 11.0, 10.7, 11.5, 11.3] # 새로운 디자인
# 기존 디자인, 새로운 디자인 각각 리스트로 할당
#독립표본 T-검정 수행
t_stat, p_value = stats.ttest_ind(group_A, group_B)
# 귀무가설: 두 디자인 간 CTR에 유의미한 차이가 없다.
print(f"T-검정 통계량: {t_stat}")
print(f"P-값: {p_value}")
if p_value < 0.01:
print("귀무가설 기각: 새로운 디자인(B)이 기존 디자인(A)보다 유의미하게 CTR이 높음")
else:
print("귀무가설 채택: 두 디자인 간 CTR 차이가 없음")
# p값이 0.01보다 작다면 귀무가설 기각, 대립가설 채택 -> 두 디자인 간 CTR에 유의미한 차이 있음.
# p값이 0.01보다 크면 귀무가설 채택 -> 두 디자인 간 CTR에 유의미한 차이 없음.

- 대응표본 T-검정
before_satisfaction = np.array([3.5, 3.7, 3.8, 3.6, 3.9, 3.4, 3.8])
after_satisfaction = np.array([4.1, 4.2, 4.0, 4.3, 4.1, 4.0, 4.2])
t_stat, p_value = stats.ttest_rel(after_satisfaction, before_satisfaction)
# 대응표본 t-검정 수행: after_satisfaction과 before_satisfaction 간의 평균 차이가 유의미한지를 검정
print(f"T-검정 통계량: {t_stat:.4f}")
print(f"p-값 (양측검정): {p_value:.4f}")
if p_value < 0.05:
print("귀무가설 기각: 온라인 수업 만족도에 유의미한 변화가 있음")
else:
print("귀무가설 채택: 만족도 변화는 통계적으로 유의하지 않음")
# p값이 0.05보다 작으면 귀무가설 기각
# p값(0.0009)이 0.05보다 작으므로 귀무가설 기각, 대립가설 채택
2. 데이터의 종류와 특성
| 종류 | 의미 | ex | |
| 정성적 데이터 (= 범주형) | 명목형 데이터 | 순서가 없음 | 혈액형, 성별 |
| 서열형 데이터 | 순서가 있음 | 고객 만족도 설문조사(매우 만족~불만족) | |
| 정량적 데이터 | 이산형 데이터 | 특정 값만 가질 수 있는 데이터 | 학생 수, 주사위 눈 |
| 연속형 데이터 | 특정 구간 내에서 무한히 많은 값을 가질 수 있는 데이터 | 온도, 키, 몸무게 |
● 데이터 분포와 확률
| 정규 분포 | 평균과 표준편차로 정의된 종 모양을 가진 대칭적인 분포 |
| 균등분포 | 모든 값이 동일한 확률을 가짐 ex) 주사위를 던질 때 각 면이 나올 확률은 동일 |
| 이항 분포 | 특정 사건이 여러 번 반복될 때, 성공과 실패의 횟수를 따지는 분포 ex) 동전을 5번 던졌을 때 앞면이 나오는 횟수 |
| 포아송 분포 | 일정 시간이나 공간 내에서 발생하는 사건의 횟수를 모델링하는 데 사용 ex) 고객이 1시간 동안 매장에 방문하는 횟수 |
| 지수 분포 | 사건이 발생하는 시간 간격을 모델 ex) 고객이 매장에 도착하는 시간 간격 |
| 감마 분포 | 지수 분포를 일반화한 분포 |
| 카이제곱 분포 | 정규 분포를 따르는 여러 변수들의 제곱합을 따르는 분포 |
# [멋사 그로스마케팅 부트캠프 DAY16] 후기 & 회고
부트캠프 듣기 전에 도움이 될거 같아 ADSP 자격증 공부를 했던게 오늘 조금 도움이 됐다. 익숙한 용어라 이해하는 건 괜찮았지만 주어진 문제를 보고 코드를 생각해 푸는 건 아직 어려웠다.. 오늘은 실습 보단 이론에 초점이 맞춰진 수업이라 정리를 어떻게 해야할지 막막했지만 내가 중요하다고 생각하는 부분만 추려 적었다. 사실 노션 정리 + 블로그까지 하니 블로그에 많은 내용을 담는 것이 어려웠다. 노션으로 정리하는 것이 훨씬 편하고 필요하면 바로 쓸 수 있으니 더 편하게 느껴졌다.

( 저는 이렇게 페이지를 거는 걸 좋아해서 페이지> 페이지 > 만들어서 정리하고 있어요! 특히 헷갈리는 코드가 너무 많아서 정리를 해두니 아 이거 이때 써야하는데 코드가 뭐였지,,? 하면 바로 찾을 수 있어서 좋습니다!!) 점점 블로그와 멀어지는 느낌이지만 일단 시작한 이상 최선을 다 해봐야지,, 24시간이 모자랍니다 증말 ㅠㅠ 또 다른 할 일을 위해..그럼 이만! 다들 화이팅입니다요!